学習指導要領の目標において、「~の見方・考え方を働かせ、~的活動を通して…」の部分(※下図)に疑問を持つ方は少なくないと思います。以下、自分なりの理解をまとめましたのでご参考になればと思います。

「見方・考え方」について
学習指導要領解説を抜粋すると以下になります。
・数学的な見方:
事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること
・数学的な考え方:
目的に応じて数,式,図,表,グラフ等を活用しつつ,論理的に考え,問題解決の過程を振り返るなどして既習の知識及び技能を関連付けながら,統合的・発展的に考えること
未だ漠然とした感じがあります。平成28年教科課程ワーキンググループの資料※1も参考にして考えてみたものが次の図になります。

表の赤文字の部分を見ると少しわかりやすいでしょうか。
深入りするために少し発想を変えて、一つの事象を複数の見方で捉えてみましょう。例えば、美しい音楽を聴いたとしましょう。楽典のような観点で捉える事は音楽的な見方になりましょう。また、西洋や東洋の文化と紐づけて考えるのは社会的な捉え方でしょうか。では、数学的な見方をするとどうなるか、、、おそらく、三角関数のような数(関数)として捉えて考えるような見方でしょう。
※社会科、音楽科の教員の方、間違っていたら申し訳ありません。
数学的な考え方はどうでしょう。例えば、学習指導要領の例では、マイナスの概念を獲得する事は既存の自然数で概念の適用範囲を広げて考える、即ち統合的に考えること、としています。安易な発想ですが、図形の問題を複素数やベクトルという別の視点から捉え直す、様なことは発展的に考える事になるのでしょう。
また、この他にもよく話題に上がる数学的な考え方としては、一般化、数理モデル化のような考え方でしょう。これも発展的に考える数学的な考え方だと私も思います。他にも、別の視点があったらコメントいただけると幸いです!
「数学的活動を通して」について
数学的活動に関しては学習指導要領解説に詳細が載っており「事象を数理的に捉え、数学の問題を見出し、問題を自立的、協働的に解決する活動」とされております。二通りの活動があるとされて一つ目は「現実世界」(図の左側のループ)を通した活動、二つ目は、「数学の世界」(図の右側のループ)を通した活動です。
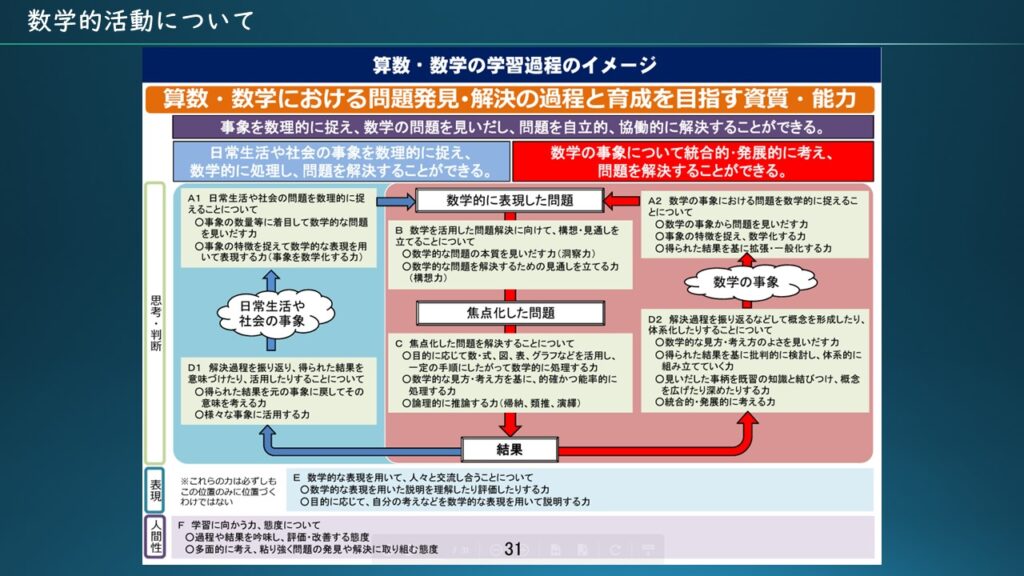
詳細は学習指導要領の解説に任せるとして、ここではなぜ数学的活動が必要なのかについて考える事にします。本稿を書こうと思ったきっかけは、なぜ数学的活動が必要なのか?という疑問を初めに抱いたためです。例えば遊びやゲームのをやっている時でも、数学的資質・能力が身に付くならそれでよいではないか?と。色々調べた結果、数学的資質・能力を身に付けるためには、遊びやゲームでもダメで、もちろん国語的活動でもダメで、数学的活動が必須だったのだ、と今は考えています。これは、当たり前のことですが、ここが重要なのではないかと思います。
つまり、数学的な資質・能力は、日常生活でも数学の世界でも問題を解こうと主体的に考え、その過程で色々試行錯誤しているうちに自然と身に付いていくものである、故に数学的な活動が必要だ、と思っています。
一つ例を考えると、一見複雑な問題を解くときに、因数分解で簡単にできないか?いや結果的には解の公式の方が早いか?はたまた、解と係数の関係で解いた方が簡単になるのでないか?と思考を巡らせます。既習の知識をフルに活用して比較して最適な手順で解こうと努力するわけです。この過程で思考の訓練がなされ数学的な考え方は鍛えられます。
また、類似の問題だが別種の問題にぶつかったとします。先の問題と比較して最適な方法何かを考えるうちに本質に気付くことを経験された方も多くいると思います。
私は、まさに、この問題を解くという数学的活動が数学的資質・能力を高めていると考えるわけです。この例では問題を解くという行為に着目しましたが、日常の事象を数学の問題に落とし込む時に、幾何学的に考えるか関数として捉えるかで悩んだりする行為も同様だと考えます。これらを図にすると、以下のイメージになるかと思います。
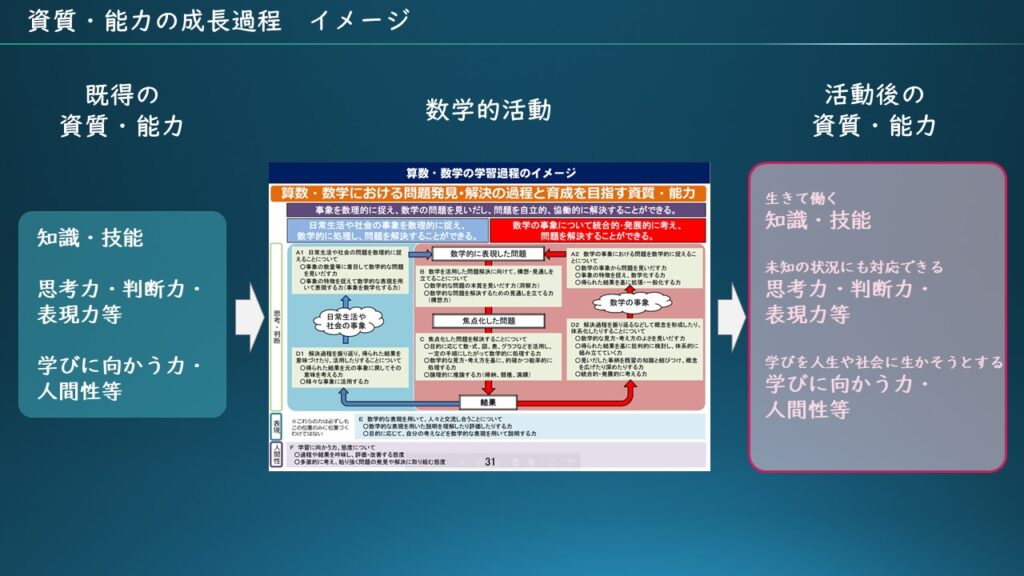
いかがでしたでしょうか。色々書きましたが、本稿が何かの気づきになっていたら幸いです。
次回は数学的な資質・能力について見ていこうと思います。




コメント